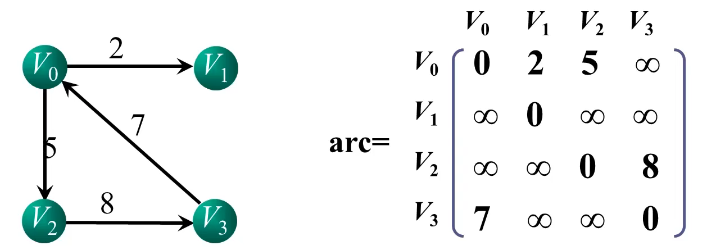图

图的定义

图是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：
$$
G=(V, E)
$$
其中：G表示一个图，V是图G中顶点的集合，E是图G中顶点之间边的集合。

 

在线性表中，元素个数可以为零，称为空表；

在树中，结点个数可以为零，称为空树；

在图中，顶点个数不能为零，但可以没有边。(没有空图的概念)

 

图的逻辑结构

若顶点$v_i$和$v_j$之间的边没有方向，则称这条边为无向边，表示为$(v_i,v_j)$。
如果图的任意两个顶点之间的边都是无向边，则称该图为无向图

若从顶点v，到v，的边有方向，则称这条边为有向边，表示为<vi，v>。
如果图的任意两个顶点之间的边都是有向边，则称该图为有向图

图的基本术语

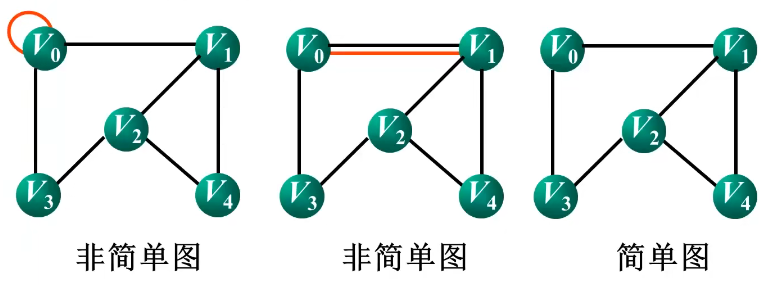
简单图：在图中，若不存在顶点到其自身的边，且同一条边不重复出现。

数据结构中讨论的都是简单图。

 

邻接,依附

无向图

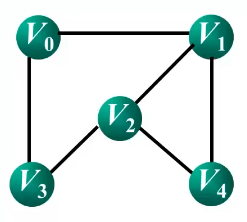
无向图中，对于任意两个顶点$v_i$，和顶点$v_j$，若存在边$(v_i,v_j)$，则称顶点$v_i$，和顶点$v_j$，互为邻接点，同时称边$(v_i,v_j)$依附于顶点$v_i$，和顶点$v_j$

$v_0$的邻接点：$v_1$,$v_3$
$v_1$的邻接点:$v_0$,$v_2$,$v_4$

有向图

无向图中，对于任意两个顶点$v_i$，和顶点$v_j$，若存在弧$<v_i,v_j>$，则称顶点$v_i$，和顶点$v_j$，互为邻接点，同时称弧$<v_i,v_j>$依附于顶点$v_i$，和顶点$v_j$

 

不同逻辑结构关系的对比

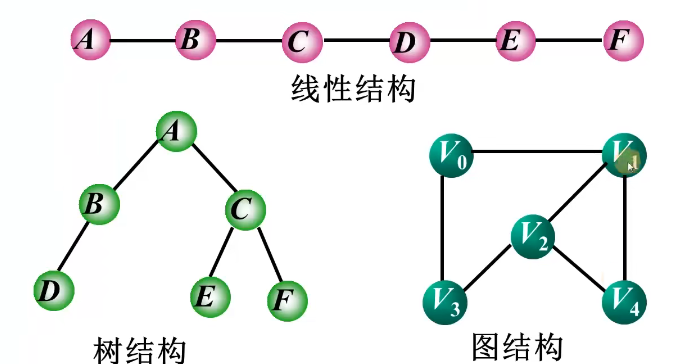
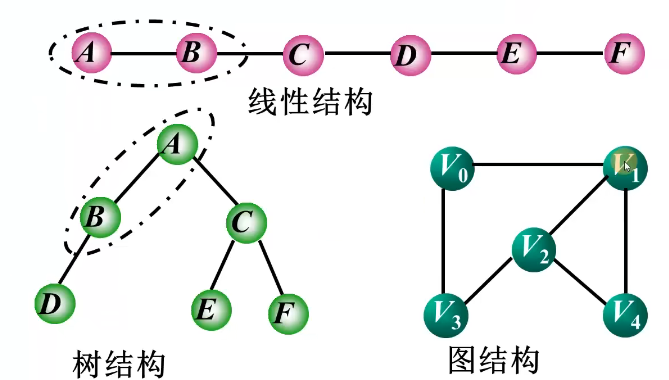
在线性结构中，数据元素之间仅具有线性关系；
在树结构中，结点之间具有层次关系；
在图结构中，任意两个顶点之间都可能有关系。

在线性结构中，元素之间的关系为前驱和后继
在树结构中，结点之间的关系为双亲和孩子
在图结构中，顶点之间的关系为邻接。
 

图的基本术语

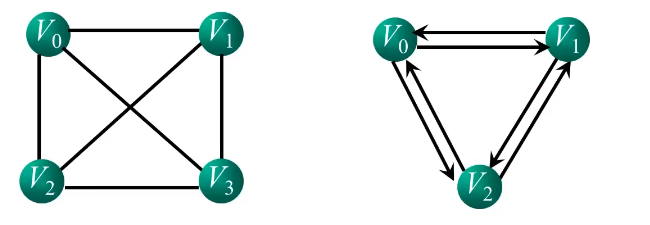
无向完全图：在无向图中，如果任意两个顶点之间都存在边，则称该图为无向完全图。
有向完全图：在有向图中，如果任意两个顶点之间都存在方向相反的两条弧，则称该图为有向完全图

含有n个顶点的无向完全图有$n\times（n-1）/2$条边。
含有n个顶点的有向完全图有$n\times （n-1）$条弧。

 

稀疏图：称边数很少的图为稀疏图；稠密图：称边数很多的图为稠密图。
顶点的度：在无向图中，顶点v的度是指依附于该顶点的边数，通常记为$TD（v）$。
顶点的入度：在有向图中，顶点v的入度是指以该顶点为弧头的弧的数目，记为$ID（v）$；顶点的出度：在有向图中，顶点v的出度是指以该顶点为弧尾的弧的数目，记为$OD（v）$。

 

在具有n个顶点、e条边的无向图中，各顶点的度之和与边数之和有如下关系
$$
\sum\limits_{i=1}^{n}T D\left(\nu_{i}\right)=2e
$$
在具有n个顶点、e条边的有向图中，各顶点的入度之和与各顶点的出度之和有如下关系
$$
\sum\limits_{i=1}^{{n}ID\left(v_i\right)=\sum\limits_{i=1}}{n}OD\left(v_i\right)=e
$$
 

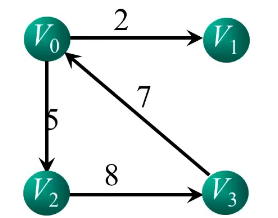
权：是指对边赋予的有意义的数值量。(一个节点到另一个结点需要的代价)
网：边上带权的图，也称网图

路的长度

非带权图 ————> 路径上边的个数
带权图 ————> 路径上各边的权之和

回路，简单路径，简单回路

回路（环）：第一个顶点和最后一个顶点相同的路径。
简单路径：序列中顶点不重复出现的路径。
简单回路（简单环）：除了第一个顶点和最后一个顶点外，其余顶点不重复出现的回路。

 

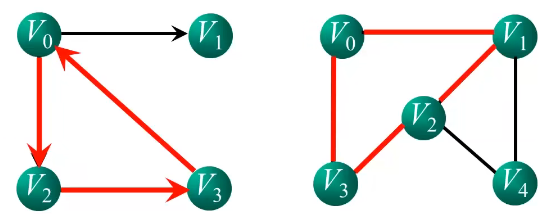
连通图，连通分量

连通图：在无向图中，如果从一个顶点$v_i$，到另一个顶点$v_j(i\ne j)$有路径，则称顶点$v_i$，和$v_j$，是连通的。如果图中任意两个顶点都是连通的，则称该图是连通图。
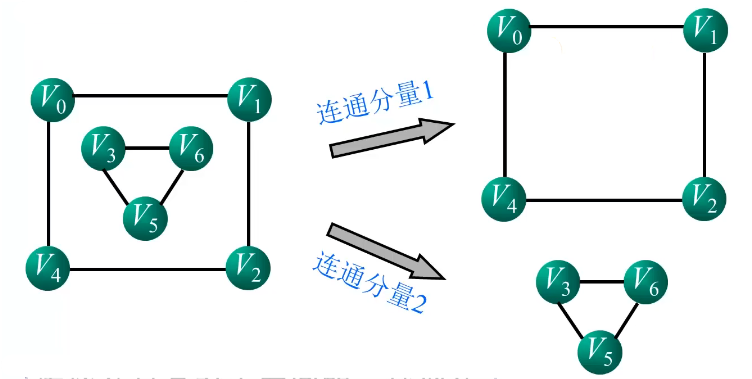
连通分量：非连通图的极大连通子图称为连通分量。

​ 1.含有极大顶点数；
​ 2.依附于这些顶点的所有边

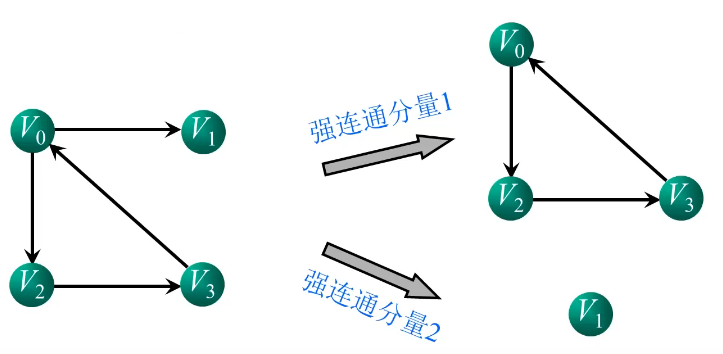
强连通图：在有向图中，对图中任意一对顶点$v_i$，$v_j(i\ne j)$，若从顶点$v_i$，到顶点$v_j$，和从顶点$v_j$，到顶点$v_i$，均有路径则称该有向图是强连通图。
强连通分量：非强连通图的极大强连通子图。

 

生成树

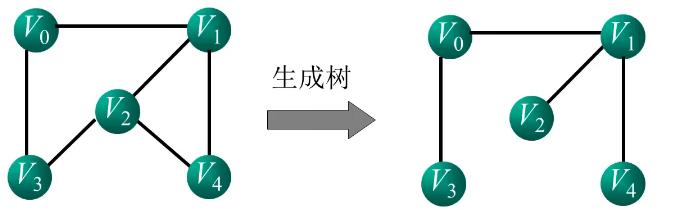
生成树：n个顶点的连通图G的生成树是包含G中全部顶点的一个$极小连通子图$。

含有n-1条边，多一条构成回路，少一条不连通

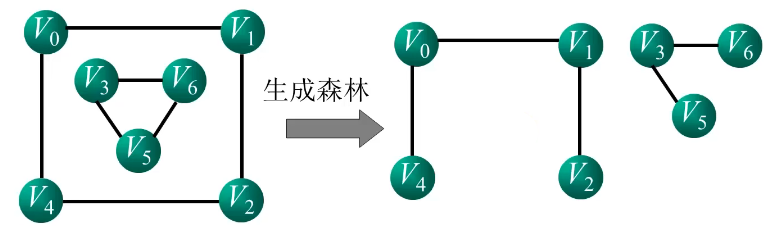
生成森林：在非连通图中，由每个连通分量都可以得到一棵生成树，这些连通分量的生成树就组成了一个非连通图的生成森林。

 

图的储存

图的粗存结构及实现

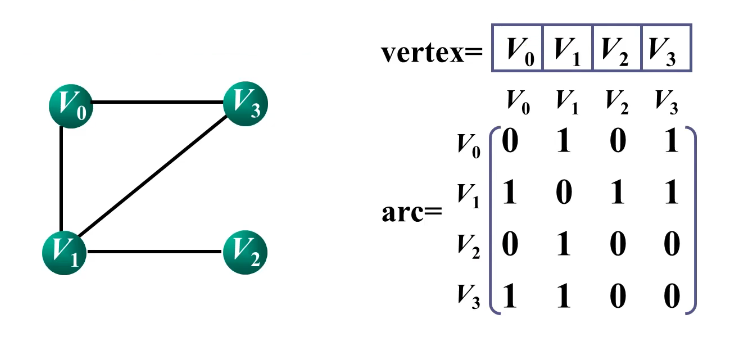
邻接矩阵

基本思想：用一个一维数组存储图中顶点的信息，用一个二维数组（称为邻接矩阵）存储图中各顶点之间的邻接关系。

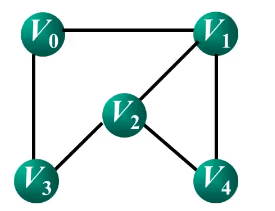
无向图的邻接矩阵

特点：

主对角线为0且一定是对称矩阵。

如何求邻接矩阵中的度

通过扫描该点邻接矩阵中的行

该点边表中结点的个数

 

有向图的临界矩阵

可能不是对称的

 

网图邻接矩阵的定义

$$
\textbf{arc}[i][j]=\left{\begin{array}{l}\boldsymbol{w}_{ij}，若(v_i,v_j)\in E(或<v_i,v_j>\in E)
\ \boldsymbol{0},若i=j
\{\infty}，其他\end{array}\right.
$$

图的储存结构及实现

const int MAX_VERTEX=10;//图的最大顶点数
class MGraph{
	private:
		Data Type vertex[MAX_VERTEX];  
		int arc[MAX_VERTEX][MAX_VERTEX];
		int vertexNum， arcNum；
	public：
		MGraph(DataType v[]，int n，int e);//构造函数
		-MGraph();           //析构函数
		void DFSTraverse(int v); //深度遍历
		void BFSTrayerse(int v);  //广度遍历
}；

 

构造函数的实现

邻接矩阵中图的基本操作——构造函数
1.确定图的顶点个数和边的个数；
2.输入顶点信息存储在一维数组vertex中；
3.初始化邻接矩阵arc；
4.依次输入每条边存储在邻接矩阵arc中；
4.1输入边依附的两个顶点的序号i，j；
4.2将邻接矩阵的第i行第j列的元素值置为1；
4.3将邻接矩阵的第j行第i列的元素值置为1；

MGraph::MGraph（Data Type v[], int n,int e）{
	vertexNum = n;
	arcNum = e;
	for （i = 0; i < vertexNum; i++）
		vertex[i] = v[i];
	for （i = 0; i < vertexNum; i++）
	//初始化邻接矩阵
		for （j = 0; j < vertexNum; j++）
			arc[i][] = 0;
	for （i = 0; i< arcNum; i++）[ //依次输入每一条边
		cin >>vi>>vj； //输入边依附的两个顶点的编号
		arc[vi][vj] = 1; //置有边标志
		arc[vj][vi] = 1;
     }
   }

邻接表

图的邻接矩阵储存结构的空间复杂度？

假设图G有n个顶点e条边，则储存该图需要$O(n^2)$

 

如果为稀疏图则会出现什么现象？

邻接表储存的基本思想：对于图的每个顶点$v_i$，将所有邻接于$v_i$的顶点链成一个单链表，称为顶点$v_i$的边表（对于有向图则称为出边表）所有边表的头指针和存储顶点信息的一维数组构成了顶点表。

 

vertex	数据域，存放顶点信息
firstEdge	指针域，指向边表中第一个结点
adjvex	邻接点域，边的终点在顶点表中的下标
next	指针域，指向边表中的下一个结点

struct ArcNode//边表
{
	int adjvex;
	ArcNode *next;
};
struct VertexNode //顶点表
{
	DataType vertex;
	ArcNode *fristEdge;
};

图的存储结构及实现

邻接表存储有向图的类

const int MAx_VERTEX = 10;
class ALGraph{
	private:
		VertexNode adjList[MAX_VERTEX];
		int vertexNum,arcNum;
	public:
		ALGraph(DataType v[],int n,int e);//构造函数
		~ALGraph();                      //析构函数
		void DFSTraverse(int v);
		void BFSTraverse(int v);
}

邻接表中图的基本操作----构造函数

1.确定图的顶点个数和边的个数

2.输入顶点信息，初始化该顶点的边表

3.依次输入边的信息并储存在边表中

​ 3.1输入边所依附的两个顶点的序号$v_i$和$v_j$

​ 3.2生成邻接点序号为$v_j$的边表结点s

​ 3.3将结点s插入到第$v_i$个边表的头部

 

ALGraph:: ALGraph(DataType v[], int n, int e){
	vertexNum = n;
	arcNum = e;
	for (i = 0; i < vertexNum; i++) {
	//初始化顶点信息，指针域都为空
		adjList[i].vertex = v[i];
		adjList[i].firstEdge = NULL;
	}
    for(i = 0;i < arcNum ;i++){
        //输入边的信息存储在边表中
        cin>>vi>>vj;//输入边依附的两个顶点的编号
        s = newArcNode;
        s->adjvex = vj;
        s->next = adjList[vi].fristEdge;
        adjList[vi].fristEdge = s;
    }
}

 

十字链表

将邻接表和逆邻接表合二为一，方便计算每个结点的入读和出度。

要频繁计算数据的入度和出度，用十字链表。

	空间性能	时间性能	适用范围	唯一
邻接矩阵	$O(n^2)$	$O(n^2)$	稠密图	唯一
邻接表	$O(n+e)$	$O(n+e)$	稀疏图	不唯一

 

图的遍历

1.在图中，任何两个顶点之间都可能存在边，顶点是没有确定的先后次序的，所以，顶点的编号不唯一。
为了定义操作的方便，将图中的顶点按任意顺序排列起来，比如，按顶点的存储顺序。

2.从某个起点始可能到达不了所有其它顶点，怎么办？

解决方案：多次调用从某顶点出发遍历图的算法。

3.因图中可能存在回路，某些顶点可能会被重复访问，那么如何避免遍历不会因回路而陷入死循环。

解决方案：附设访问标志数组visited[n]

4.在图中，一个顶点可以和其它多个顶点相连，当这样的顶点访问过后，如何选取下一个要访问的顶点？

深度和广度优先遍历

深度优先遍历

（1）访问顶点v；
（2）从v的未被访问的邻接点中选取一个顶点w，从w出发进行深度优先遍历；
（3）重复上述两步，直至图中所有和v有路径相通的顶点都被访问到。

伪代码

1.访问顶点v；visited[v]= 1；
2.w=顶点v的第一个邻接点；
3.while（w存在）
3.1 if（w未被访问）从顶点w出发递归执行该算法；
3.2 w=顶点v的下一个邻接点；

邻接表实现

void ALGraph::DFSTraverse(int * visited) {
	
	int i;
	for (i = 0; i < vertexNum; i++) {
		visited[i] = 0;
	}
	for (i = 0; i < vertexNum; i++) {  //循环遍历每个顶点
		if (!visited[i]) {
			DFS(i, visited);
		}
	}
}

void ALGraph::DFS(int v, int *visited) {   //遍历单个头顶点

	visited[v] = 1;
	cout << adjList[v].vertex << " ";
	ArcNode *p = adjList[v].firstEdge;
	while (p) {
		if (!visited[p->adjvex]) {
			DFS(p->adjvex, visited);
		}
		p = p->next;
	}

}

邻接矩阵实现

template<class T>
void MGraph<T>::DFS(int i,int * visited){
	cout<<vertex[i]<<" ";
	visited[i] = 1;
	for(int j=0;j<vertexNum;j++){
		if(visited[j] == 0&&arc[i][j] != 0 &&arc[i][j] != INFINIT){
			DFS(j,visited);
		}
	}
}

template<class T>
void MGraph<T>::DFSTraverse(int * visited){
	for(int i=0;i<vertexNum;i++){
		visited[i] = 0;
	}
	for(int i=0;i<vertexNum;i++){
		if(!visited[i]){
			DFS(i,visited);
		}
	}
}

广度优先遍历

基本思想：
（1）访问顶点v；
（2）依次访问v的各个未被访问的邻接点v1，V2，…，Vk
（3）分别从v1，V2,…, Vk出发依次访问它们未被访问的邻接点，并使“先被访问顶点的邻接点”先于后被访问顶点的邻接点”被访问。直至图中所有与顶点v有路径相通的顶点都被访问到。

邻接表实现

void ALGraph::BFSTraverse(int * visited) {
	
	int i;
	for (i = 0; i < vertexNum; i++) {
		visited[i] = 0;
	}
	for (i = 0; i < vertexNum; i++) {
		if (!visited[i]) {
			BFS(i, visited);
		}
	}
}

void ALGraph::BFS(int i, int *visited) {
	queue<int> q;
	visited[i] = 1;
	q.push(i);
	
	while(!q.empty()){
		int temp = q.front();
		cout<<adjList[temp].vertex<<" ";
		q.pop();
		ArcNode * p = adjList[i].firstEdge;
		while(p){
			if(!visited[p->adjvex]){
				q.push(p->adjvex);
				visited[p->adjvex] = 1;
			}
			p = p->next;
		}
	}
	
}

邻接矩阵实现

template<class T>
void MGraph<T>::BFS(int i,int * visited){
	queue<int> q;
	visited[i] = 1;
	q.push(i);
	while(!q.empty()){
		int temp = q.front();
		cout<<vertex[temp]<<" ";
		q.pop();
		for(int j=0;j<vertexNum;j++){
			if(!vertex[i]&&arc[i][j]!=0&&arc[i][j]!=INFINIT){
				
				visited[j] = 1;
				q.push(j);
			}
		}

	}
	cout<<endl;
}
template<class T>
void MGraph<T>::BFSTraverse(int * visited){
	for(int i=0;i<vertexNum;i++){
		visited[i] = 0;
	}
	for(int i=0;i<vertexNum;i++){
		if(!visited[i]){
			BFS(i,visited);
		}
	}
}

 

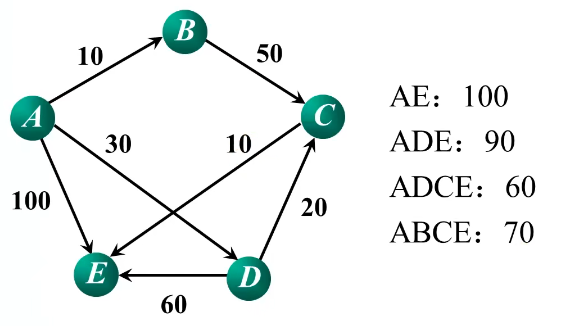
最短路径—Dijkstra算法

在网图中，最短路径是指两顶点之间经历的边上权值之和最短的路径。

单源点最短路径问题

问题描述：给定带权有向图G=（V，E）和源点v$\in $V，求从v到G中其余各顶点的最短路径。

图的存储结构：带权的邻接矩阵存储结构

数组dist[n]：每个分量dist[i]表示当前所找到的从始点v到终点$v_i$，的最短路径的长度。初态为：若从v到$v_i$，有弧，则dist[i]为弧上权值；否则置dist[i]为$\infty $。
数组path[n]： path[i]是一个字符串，表示当前所找到的从始点v到终点$v_i$，的最短路径。初态为：若从v到
$v_i$有弧，则path[i]为0；否则置path[i]为-1。
数组s[n]：存放源点和已经生成的终点，其初态为只有一个源点v。

 

伪代码

1.初始化数组dist、path和s；

2. while （s中的元素个数<n）
   2.1 在dist[n]中求最小值，其下标为k；
   2.2 输出dist[j]和path[jl；
   2.3修改数组dist和path；
   2.4将顶点$v_k$添加到数组s中；